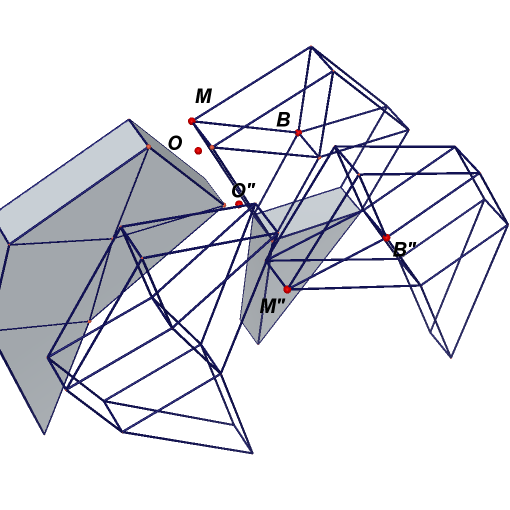
The Theo Jansen Mechanism is simply a combination of a four-bar mechanism (Crank-Rocker) with a another four-bar mechanism that create a motion similar to gait motion at the end-effector. Click right picture to see the animation. The following is a detailed construction process.
1. Start with a point A on z-axis.
2. Draw a line parallel to
y-axis through A. Take a point B on the line such that
=
4.174 
.
3. Draw a circle in yz-plane centered on point O of radius 1.543
.
Take a movable point M on the circle.
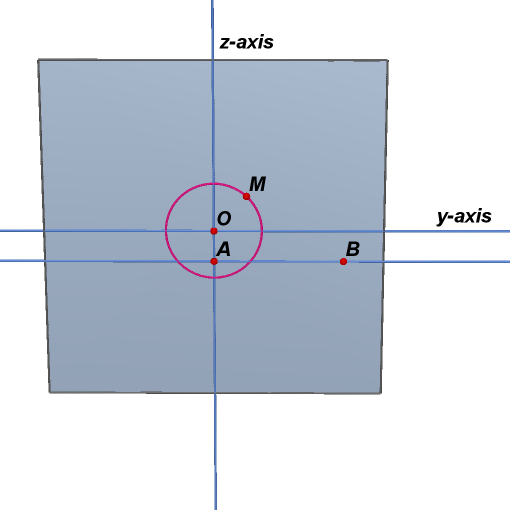
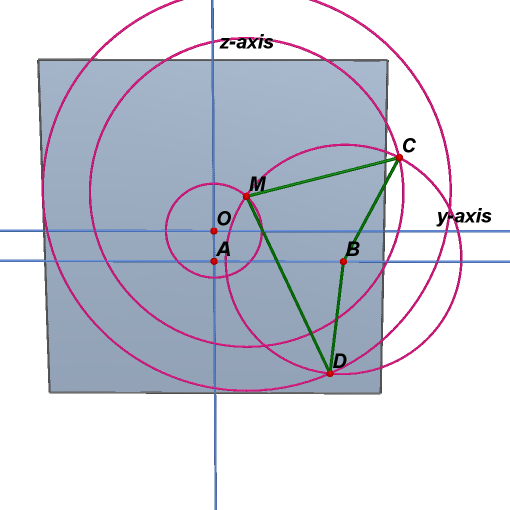
4. In yz-plane, draw
circle centered M of radius 5.006
,
circle centered M of radius 6.513
,
and circle centered B of radius 3.799
.
Point C is the higher one of intersections of first and third circles.
Point D is the lower one of intersections of second and third circles.
5. Connect segment MC, MD, BC, and BD.
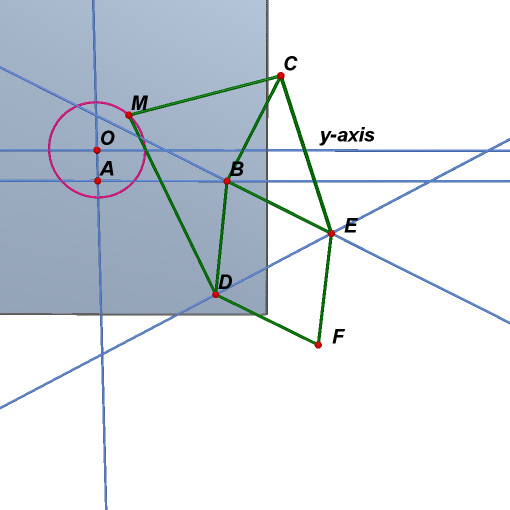
6. Hide previous three circles.
7. Draw a line in yz-plane
perpendicular to segment BC. Point E is on the line such that
=
.
8. Draw a line through D and E. Point F is the reflection of point B around line DE.
9. Connect segment CE, BE, EF, and DF.
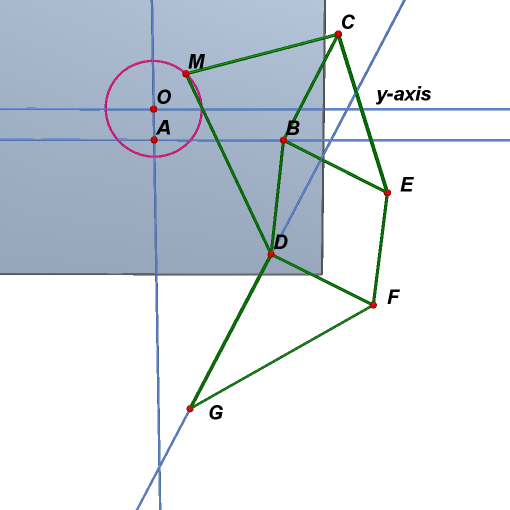
10. Hide previous two lines.
11. Draw a line in yz-plane perpendicular to segment DF. Point G is on the line such that
=
6.005 . 
12. Hide previous line.
13. Take a point M' central symmetry of M through O. Reflect point B around z-axis to get point B'.
14. Repeat steps 4~11 to point M' and point B'.
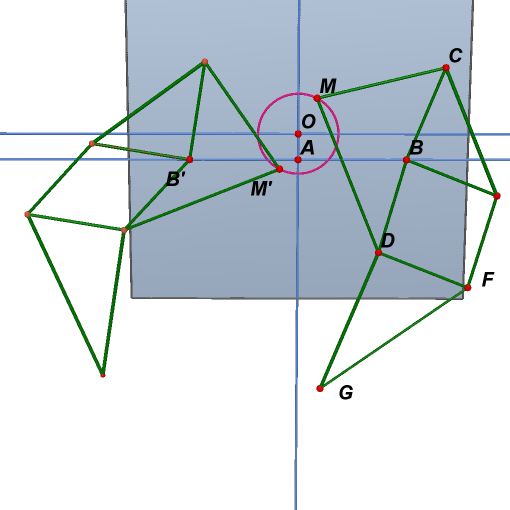
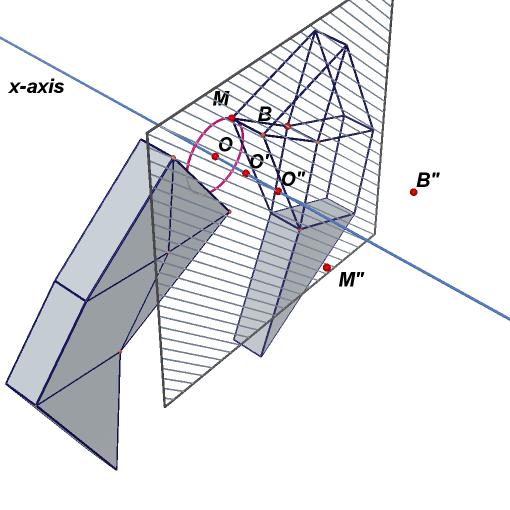
15. Hide the yz-plane, and draw the x-axis.
16. Take a suitable point O' on x-axis. Translate all segments mapping point O to point O'. Take convex polygons constructed by corresponding segments.
17. Point O'' is the central symmetry of O through O'. Point M'' is the central symmetry of M through O''.
18. Create a plane perpendicular to x-axis through O''. Reflect point B in this plane to obtain B''.
